Recursion遞迴

遞迴是那些聽起來比實際更令人生畏的概念之一。老實說。要利用它，你不需要掌握複雜的數學思想;或者從四個維度開始思考;或者一個接一個地接受某個人的夢想將一個想法植入他們的潛意識中，或甚至理解遞迴的含義。

在大多數情況下，遞迴的許多用法都有很好的參考文件和實例。然後，你可以將它們複製並貼上到程式碼中，而無需了解它們的運作的方式，也不用知道它們為什麼要這樣做。但如果你這樣做，你會錯過很有意思的遞迴。在編寫幾行程式碼後，遞迴是讓CPU完成困難度高的工作的最佳方法之一;因此，它可以幫助你避免在沒有遞迴的情況下需要或可能去解決更複雜的問題。

這是因為遞迴是通過重複一個簡單函數來解決更複雜問題的一種方法。訣竅是這個功能函數從內部作迴圈。它不是從另一個函數起動運行原函數，而是從自己的代碼中調用自己的另一個自己。這種programming相當於將兩個鏡像子面對面創建出看似無限的鏡子，遞迴的一個經典且最簡單的示例是一個函數的階乘。正整數的階乘。例如，4的階乘是4x3x2x1，等於24

#用for寫階乘

<?php
function factorial($n){
    $result = 1;
    for ($i=2; $i<=$n; $i++) {
            $result *= $i;
    }
return $result;
}
echo factorial(4);
?>

#用遞迴寫階乘
<?php
function factorial($n) {
    return $n == 0 ? 1 : $n*factorial($n-1);
}
echo factorial(4)."<br>";
?>

#費氏數列Fibonacci Sequence:
兔子繁殖說明

Fn=Fn-1+Fn-2,n>=3
F1=F2=1

1->1->2->3->5->8->13->21(從3開始每一項都是前兩項之和)

#python費氏數列:
def Fib(n):
if n == 0:
return 0;
elif n == 1:
return 1;
return Fib(n-1) + Fib(n-2)

print(Fib(4))

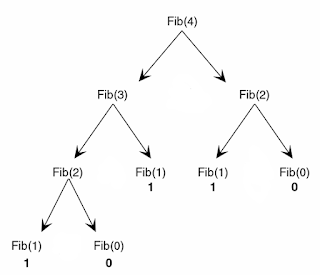
#遞迴樹Recusive Trees
從上面的圖可以觀察到，每一次函式往下的呼叫，最後都會停在 Fib(1) 或 Fib(0)，因為這兩項是唯一在計算費氏數列時先被定義的。因此找到這兩項後，就可以開始往前加總出其他項的值，而往前加總的順序如下：

由圖可知Fib(4)共呼叫9次
f(0) = 0 , 1次
f(1) = 1 , 1次
f(2) = f(0) + f(1) , 1+1+1=3 次
f(3) = f(2) + f(1) , 3+1+1=5 次
f(4) = f(3) + f(2) , 5+3+1=9 次

因此導出呼叫次數為 "f(n)=f(n-1)+f(n-2)+1"
就費氏數列後面再加個1就是答案了  

自然界實例
有趣的是，如果初生結構之間的角度是黃金角度，螺旋線的數目就往往是「費氏數列」中的數。費氏數列最先由13世紀的意大利數學家萊奧納爾多·斐波那契提出。這個數列中，在1之後的每個數都是前兩個數的和，即是1,1,2,3,5,8,13,21,34,55……如此類推。

許多呈螺旋圖案的植物，花瓣數目往往是費氏數列中的數。有些人觀察到，毛茛的花有5塊花瓣，美洲血根草有8塊，柳蘭有13塊，紫菀有21塊，春白菊有34塊，美國紫菀則有55塊或89塊。（圖六）在水果和蔬菜中也可以找到跟費氏數列有關的數字。例如，香蕉的橫切面是一個五邊形。