二元樹&排序Binary search tree

演算法 & 資料結構

#自己的定義
電腦的資料說穿了就只有0和1，怎麼擺放0和1就是資料結構。
怎麼用和算就是演算法。

電腦要如何完成「排序」(sort) 這件工作呢？「二元樹」 (binary tree) 怎樣子應用在排序這項工作呢？

二元樹是數據結構。 它的關鍵特徵是樹中的每個節點最多可以有兩個子節點，它們按值排列，左邊的子節點值較低，右邊節點較高。

樹狀結構Trees

樹柱結構是一種非線性結構。例如族譜，組織架構。在資料科學方面可以應用到電腦的作業系統和資料庫管理。像我們最常看的排序就是一種運用。

Decision tree

當然機器學習中的決策樹也是一種應用

Binary Tree: Traversal(尋訪)

連結串列Linked list

樹的結構與規範

01. 樹根root

02.節點node

node為n個互斥的集合，n>=0，互斥的集合也是一棵樹稱為子樹

03.不能有重邊

04.不能有迴圈

05.不能不連通

06. 分支度(Degree)

07. 階層(Level)

08. 高度(Height)

09. 終端節點(Terminal Nodes)

10. 父節點(Parent)

11.  子節點(Children)

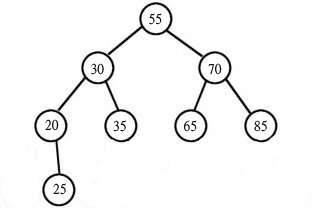
建立一排數列為: 55,70,30,65,20,25,35,85

*中序法依序排列

root=55

70>55,在55右邊

30<55,在55左邊

65>55,在55右邊,但65<70,在70左邊

以此類推

#python二元樹排序

*定義Tree

class Node:
         def __init__(self, val):
            self.l_child = None
            self.r_child = None
            self.data = val

*插入node

r = Node(55)
binary_insert(r, Node(70))
binary_insert(r, Node(30))
binary_insert(r, Node(65))
binary_insert(r, Node(20))
binary_insert(r, Node(25))
binary_insert(r, Node(35))
binary_insert(r, Node(85))

def binary_insert(root, node):
       if root is None:
             root = node
       else:
           if root.data > node.data:
                  if root.l_child is None:
                        root.l_child = node
                  else:
                        binary_insert(root.l_child, node)
           else:
                  if root.r_child is None:
                        root.r_child = node
                  else:
                        binary_insert(root.r_child, node)

def in_order_print(root):
       if not root:
             return
       in_order_print(root.l_child)
       print(root.data)
       in_order_print(root.r_child)

def pre_order_print(root):
       if not root:
             return
       print(root.data)
       pre_order_print(root.l_child)
       pre_order_print(root.r_child) 

in_order_print(r)